


















Gambling
Copyright © August 8, 2024 by Robert Wayne Atkins, P.E.
All Rights Reserved.
Introduction
 To the average person the word "gambling" may evoke images of a casino, or a dice (craps) table, or a roulette wheel, or a blackjack table, or a race track, or a state lottery ticket, or something else.
To the average person the word "gambling" may evoke images of a casino, or a dice (craps) table, or a roulette wheel, or a blackjack table, or a race track, or a state lottery ticket, or something else.
Most people know that gambling involves putting some of your money at risk and that you will lose your money if you don't win.
This short article will not discuss the pros and cons of gambling.
Instead this short article will attempt to clarify the chance of winning if you gamble with your money.
State Lottery Tickets
The odds of winning a state lottery is relatively easy to predict based on how many numbers are involved.
Let's consider two common examples:
Example One:
A state lottery has 10 ping pong balls with a number between 0 to 9 on each ball. There is only one number on each ball. When the lottery is conducted, four balls are drawn at random and they are placed on a pedestal in the exact order in which they were drawn. The resulting 4-digit number is the winning number in the lottery. How many different lottery numbers are possible?
Answer:
In mathematics this would be an example of a permutation where capital "P" represents the number of permutations or possible outcomes.
n = 10 = total number of ping pong balls.
r = 4 = number of ping pong balls selected.
The permutation equation is:
nPr = n!/(n-r)!
10P4 = 10! / (10-4)! = 10! / 6!
10P4 = 3,628,800 / 720 = 5,040
You can verify the above answer by using the internet to calculate the number of "permutations" using the values of 10 and 4.
Interpretation:
There are 5,040 possible 4-digit numbers when the sequence is important but the individual numbers 0 to 9 cannot repeat. In other words, the number 2,384 is possible but the number 2,333 is not possible because it contains more than one 3.
Therefore a person has 1 chance of winning out of 5,040 chances. In other words, on the average a person will win one time for every 5,040 times the person plays the game. If a person plays the game every day, then the person will win one time in 13.8 years (5,040 / 365 days per year). If the amount of money won is less than $5,040 then the person will be a net loser assuming that $1 is invested for each lottery ticket.
Example Two:
A state lottery has 46 ping pong balls with a number between 1 to 46 on each ball. Only one number is on each ball. When the lottery is conducted, six balls are drawn at random and placed on a pedestal. The winning lottery number is any lottery ticket that contains all six numbers, regardless of the sequence of the numbers. How many different lottery numbers are possible?
Answer:
In mathematics this would be an example of a combination where capital "C" represents the number of combinations or possible outcomes.
n = 46 = total number of ping pong balls.
r = 6 = number of ping pong balls selected.
The combination equation is:
nCr = n! / (r! (n-r)!)
46C6 = 46! / (6! (46-6)!) = 46! / (6! 40!) = 9,366,819
You can verify the above answer by using the internet to calculate the number of "combinations" using the values of 46 and 6.
Interpretation:
There are 9,366,819 different lottery numbers when the sequence is not important and the numbers cannot repeat. In this situation a number only has to be included in the six numbers chosen and it doesn't matter if it is the first or last number chosen.
(Note: A "power ball" lottery uses a slightly different method to calculate the number of options.)
Therefore a person has 1 chance of winning out of 9,366,819 chances. In other words, on the average a person will win one time for every 9,366,819 times the person plays the game. If a person plays the game every week, then the person will win one time in 180,131 years (9,366,819 / 52 weeks per year).
Casinos and the Game of Roulette
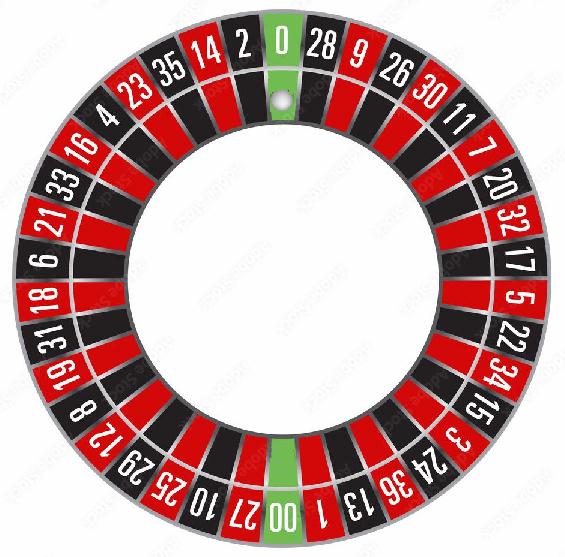 In the USA a roulette wheel has 38 slots.
In the USA a roulette wheel has 38 slots.
The numbers 1 to 36 appear in 36 of the slots at random locations around the wheel.
The number zero is in one slot and the number 00 is in one slot.
The numbers 0 and 00 are the casino numbers and they are green.
Half of the numbers 1 to 36 are red and half are black.
Half of the numbers 1 to 36 are odd and half are even.
Betting: In the following examples we will assume that a one dollar bet is placed on each spin of the wheel.
Example Three:
Betting Individual Numbers 0, 00, or 1 to 36:
If you bet on one number and the ball lands in the slot with your number then you win 35 times your bet.
Since there are 38 slots on the roulette wheel, your chance of winning is 1/38 or on the average you will win one time for every 38 spins of the wheel and when you win you will receive 35 dollars.
Your chance of losing is 37/38 and you will lose one dollar on 37 of the 38 spins of the wheel.
Therefore, on the average, after 38 spins you will have lost 37 dollars and you will have won 35 dollars. Your net loss will be 2 dollars.
Example Four:
Betting on Odd or Even:
18 numbers are odd and 18 numbers are even.
0 and 00 are neither odd or even.
If you bet on "odd" then on the average you will win 18 times out of 38 spins of the wheel and you will lose 20 times out of 38 spins.
Therefore, on the average, after 38 spins you will have won 18 dollars and lost 20 dollars. Your net loss will be 2 dollars.
The same math applies if you decide to bet on "even."
Example Five:
Betting on Red or Black:
16 numbers are red and 16 numbers are black.
0 and 00 are green.
If you bet on "red" then on the average you will win 18 times out of 38 spins of the wheel and you will lose 20 times out of 38 spins.
Therefore, on the average, after 38 spins you will have won 18 dollars and lost 20 dollars. Your net loss will be 2 dollars.
The same math applies if you decide to bet on "black."
Example Six:
There are a lot of other possible ways to place bets on a roulette table.
But if you will do the math you will discover that regardless of how you bet your net loss on the average will be 2 dollars per 38 spins of the wheel.
Summary of Casino Games
It is possible to mathematically prove that the odds are in favor of the casino on every game in the casino, including blackjack, craps, and the slot machines.
If a person wishes to gamble then the person may do so. Occasionally the person will win. But in the long run the person always, always loses.
The exception is the person who wins the casino's "jackpot" or a state's "big lottery." But this only happens to one person out of many millions of people. In other words, the casino and the state never lose money in the long run.
People who enter a casino with a "system" to beat the casino never win. The reason is because the odds are always in favor of the casino and no "system" can change those odds. If every bet in the casino is a loser in the long run, then there is no way to create a long run winner out of some combination of long run losers.
The Stock Market
There are several different stock exchanges in the USA. And there are stock exchanges in other countries all around the world.
When a company originally sells its stock to investors, then the company receives the money that the investors paid for the stock. However, from that time forward the stock no longer belongs to the company and the price of that stock can rise or fall depending on a lot of different variables.
Until the early 1990s most of the stocks that were sold in the USA were evaluated based on their Price/Earnings Ratio or on their Dividend Yield. But in the early 1990s stocks began to be sold based on whatever people "imagined" the stock was worth.
Individual investors and mutual funds and insurance companies and banks have sometimes made money and sometimes lost money in the stock market. Some individual investors and some large investment companies have gone bankrupt as a result of investments in the stock market.
Although most people will never believe it, the stock market is managed just like a casino. The stock market is manipulated to separate people, including large investment companies, from their money. But the people who do the "manipulating" never lose money because they pocket the money lost by investors.
The price of a stock is controlled in different ways on different stock exchanges. Some stocks have a person who controls the price of the stock based on the number of shares being bought and sold during a specific time period. The person uses a computer to set the "bid" and the "ask" price of a stock and the difference between those two numbers is revenue for the person. Some stock prices are actually controlled by computers except when the proposed change in price exceeds a specific percentage and then a person has to make a decision. Many years ago this person would purchase a "seat" on the stock exchange. Today the person may be called a "specialist" or a "market maker." The computer, or person, has access to all the current "buy" and "sell" orders. Some of these orders are entered at the current market price and the buy or sell takes place almost immediately at whatever that current market price might be. But many of the orders are at a fixed "buy" price and if that market price is actually hit then the buy takes place. And many orders are at a fixed "sell" price and if that market price is actually hit then the sell takes place. It is easy for a computer to maximize the money in the account of a "specialist" by raising the market price a little to trigger a lot of "buy" orders and then move that money into the specialist's account. Then the computer can lower the market price a little to trigger a lot of "sell" orders and then transfer some money out of the specialist's account. This creates a positive cash flow into the account of the "specialist."
It is also easy to take advantage of human greed and to gradually but systematically increase the market price of a stock over several months. Each day the market price will go up a little and down a little during the day so that the account of the "specialist" increases based on the difference between the "ask" and "sell" prices. But the long term trend will be up. When the "specialist" believes that the stock has been "milked" as much as possible, then the specialist will allow the stock price to collapse. Each day lots of people will be selling the stock but the price they sell for will be significantly less than the price they paid for the stock. The money in the account of the "specialist" will decrease each day but at the end of the "blood bath" the account of the specialist will still contain a lot more money than when the specialist began the maneuver. The specialist also knows that lots and lots of people will continue to hold onto their stock because they will refuse to take a loss (this would impact their self image) and they will continue to watch their money gradually disappear because they have convinced themselves that one day the price of their stock will go up to the price that they originally paid for the stock. Unfortunately they are almost always, always wrong. But sometimes inflation over a twenty or thirty year period will cause the entire stock market to go up and the price of their stock will also go up. But 30 years from now the purchasing power of their money will only be a tiny fraction of what it is today. The specialist also knows that large blocks of the stock were purchased by mutual funds, pension funds, and insurance companies and that these organizations do not have to flexibility to easily liquidate their stocks without getting a lot of approvals. This allows the price of the stock plenty of time to decrease even more before these large organizations can take corrective action.
People and mutual funds and pension funds and insurance companies that play the stock market are said to be "investing" in the stock market. Changing the word from "playing" to "investing" is just using a fancy word for "gambling."
Sometime in the not too distant future many people worldwide will realize what people realized in 1929. Almost all of the money they "invested" in the stock market will be gone forever. They will still own their stock certificates and they will still be legal owners of a company, but their stock certificates will only be worth a few pennies on the dollar (depending on how much they paid for the stock certificates). Or their stock certificates will become worthless if the company has gone bankrupt. This happened to my grandfather in the 1930s and I still have his paper stock certificate as a reminder of what can happen when the stock market crashes.
Digital Currencies
Digital currencies are a Ponzi scheme.
A digital currency is simply an electronic number inside a computer. An electron does not have any intrinsic value. However, you have to pay "real money" to buy some of those electrons.
As long as a Ponzi scheme is working correctly then almost nobody realizes that they have been seduced into investing in a Ponzi scheme.
Therefore most people refuse to believe that their digital currencies could become worth "nothing" in less than one second.
Individuals and companies that put their money into digital currencies are "gambling" even if they refuse to use that word.
Conclusion
Some of the people who purchase lottery tickets or visit a casino will not risk more money than they can afford to lose.
However, some of the people who purchase lottery tickets or visit a casino lose more money than they can afford to lose and the person suffers for it. Sometimes the person's family also suffers. For these people gambling is a disease that is slowly destroying their lives.
People who buy stocks or digital currencies perceive themselves as being "wise investors" and it is very difficult for them to see themselves as gamblers.
However, the people who have lost their life savings, or all their retirement money, in one of these types of investments now have a more realistic perspective on the true value of these investments.
You are an adult and you may do whatever you wish with your money.
But if you have read this article then you should not be surprised if you decide to gamble and one day you discover that you are bankrupt.
Respectfully,
Grandpappy.
Footnote:
A long time ago I read the following story somewhere but I don't remember where. And I don't know if the following story is true or not. But I thought it would be a reasonable addition to the above article.
A widow woman contacted her local Better Business Bureau to file an official complaint about a company that had legally swindled her out of her life savings.
The representative of the Better Business Bureau asked her, "Why didn't you contact us before you gave them your money?"
The widow replied, "Because I knew you would tell me not to do it."
Grandpappy's e-mail address is: RobertWayneAtkins@hotmail.com








































 To the average person the word "gambling" may evoke images of a casino, or a dice (craps) table, or a roulette wheel, or a blackjack table, or a race track, or a state lottery ticket, or something else.
To the average person the word "gambling" may evoke images of a casino, or a dice (craps) table, or a roulette wheel, or a blackjack table, or a race track, or a state lottery ticket, or something else. In the USA a roulette wheel has 38 slots.
In the USA a roulette wheel has 38 slots.
